【基本情報】コードあり！科目B「二次元配列を疎行列に変換するプログラム」について解説

基本情報技術者試験の午後問題が変わりました．
以前よりもプログラムを読み取る力が求められるようになりましたね．

科目B問題を解けるようになるにはプログラムを元に自分でコードを書いてみるのが1番良いでしょう．

今回は問4「二次元配列を疎行列に変換するプログラム」の解説とそのコードを紹介します．

Pythonで書いてみたので是非手元で実行してみてください．

科目Bサンプル問題問4 二次元配列を疎行列に変換するプログラム
まとめ

科目Bサンプル問題問4 二次元配列を疎行列に変換するプログラム

問題文は以下のとおりです．

2次元配列を使うと複雑そうに見えますね．

科目Bサンプル問題[科目B]問4 二次元配列を疎行列に変換するプログラム

2次元配列は難しそうに感じます．
しかし2次元配列も基本は配列と一緒です．

配列は各要素に数字や文字列が入ります．
2次元配列はこの各要素が配列になるだけです．

配列の中に配列が入ったものを2次元配列と呼びます．（難しそうな概念は抜きして簡単に説明すると）

プログラムをPythonで書き直す

問4に掲載されているプログラムを元にPythonで書き直しました．

プログラムと比較すると一部処理内容が異なります．
これはプログラムとPythonでインデックスの初期値が異なることが原因です．

if (matrix[i][j] != 0):
  sparseMatrix[0].append(i + 1) # プログラムでは+1不要
  sparseMatrix[1].append(j + 1)

プログラム：配列のインデックスは1から始まる
Python：配列のインデックスは0から始まる

from typing import List

# 2次元配列
matrix = [
    [3, 0, 0, 0, 0],
    [0, 2, 2, 0, 0],
    [0, 0, 0, 1, 3],
    [0, 0, 0, 2, 0],
    [0, 0, 0, 0, 1]
]

# 与えられた行列を整数型配列の配列に変換する
def transformSparseMatrix(matrix: List[List[int]]):
    
    # 要素数が0の配列を3つ持つ2次元配列
    sparseMatrix = [
        [],
        [],
        []
    ]
    
    for i in range(0, len(matrix)): # 外側の配列をループする
        for j in range(0, len(matrix[i])): # 内側の配列をループする
            if (matrix[i][j] != 0): # 内側の配列が0でないとき
                sparseMatrix[0].append(i + 1) # sparseMatrixの1つ目の配列にi+1の値を追加する
                sparseMatrix[1].append(j + 1) # sparseMatrixの2つ目の配列にj+1の値を追加する
                sparseMatrix[2].append(matrix[i][j]) # sparseMatrixの3つ目の配列にmatrix[i][j]の値を追加する
    
    return sparseMatrix # 作成した2次元配列を返す

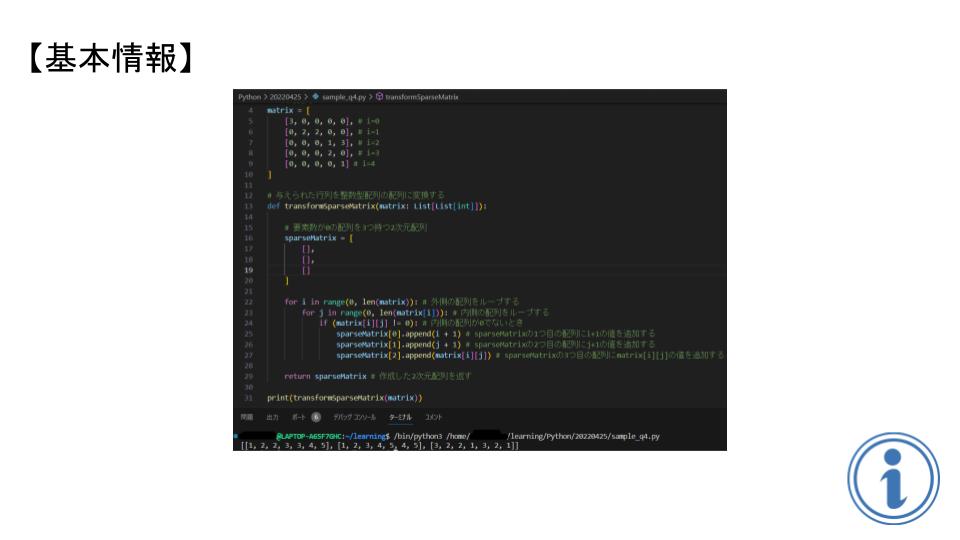
print(transformSparseMatrix(matrix))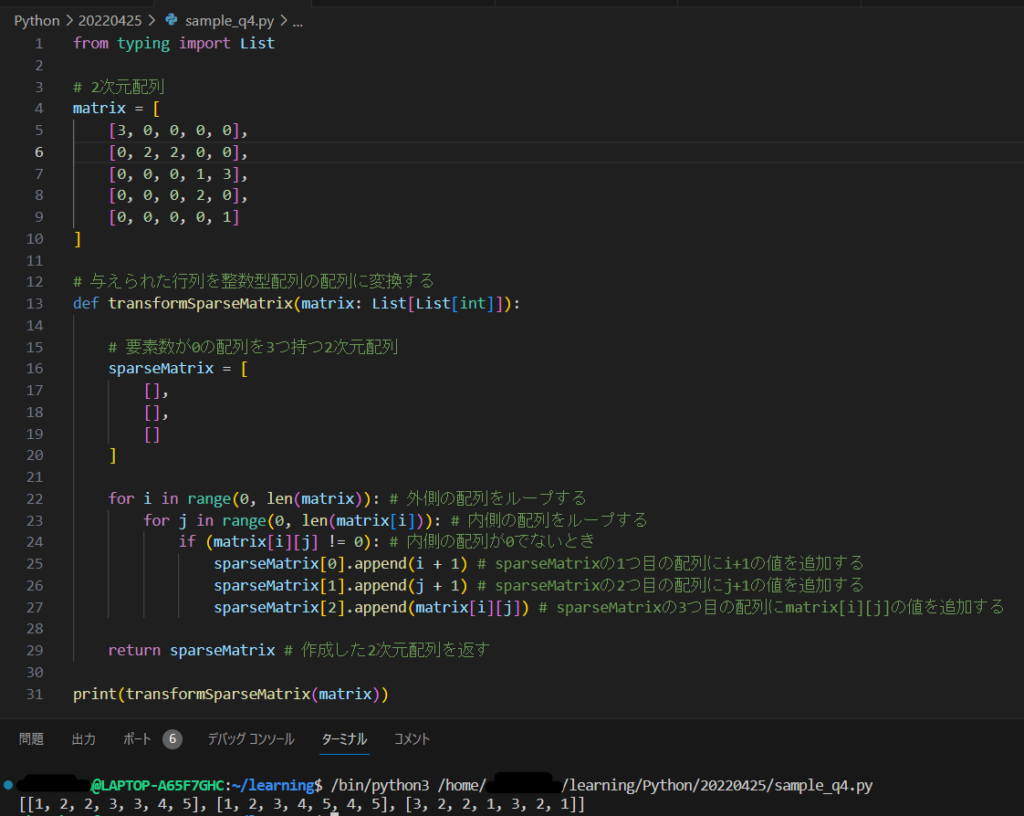

指定した値を持つ2次元配列を引数としてプログラムを実行しました．

回答である「イ」[[1, 2, 2, 3, 3, 4, 5], [1, 2, 3, 4, 5, 4, 5], [3, 2, 2, 1, 3, 2, 1]] と一致しましたね．コードに誤りはなさそうです．

ポイントとなる点を紹介します．

ポイント1. 2次元配列は見やすく区切る

関数 transformSparseMatrix を transformSparseMatrix({{3，0，0，0，0}，{0，2，2，0，0}，{0，0，0，1，3}，{0，0，0，2，0}，{0，0，0，0，1}})として呼び出したとき
科目Bサンプル問題 [科目B]問4

問題文を見ると2次元配列は1行で表記されていました．
これだとどこまでが1つの要素が分かりにくいですね．

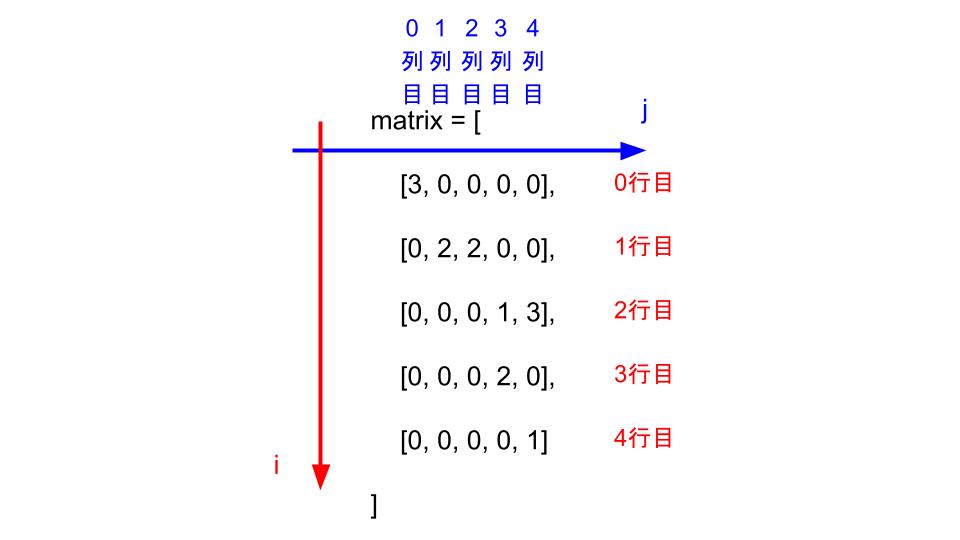
2次元配列は2つの配列から構成されています．
ここでは1つ目の配列を外側の配列，2つ目を内側の配列と呼ぶことにしましょう．

# 2次元配列
matrix = [ # 1つ目の配列（外側）
    [3, 0, 0, 0, 0], # 2つ目の配列（内側）
    [0, 2, 2, 0, 0],
    [0, 0, 0, 1, 3],
    [0, 0, 0, 2, 0],
    [0, 0, 0, 0, 1]
]

内側の配列がひとまとまりになるように区切れば構成が一目瞭然です．

問題を解くときは見やすくように書き直すと良いでしょう．

ポイント2. 2重ループの処理内容を整理する

for i in range(0, len(matrix)): # 外側の配列をループする
  for j in range(0, len(matrix[i])): # 内側の配列をループする
    if (matrix[i][j] != 0): # 内側の配列が0でないとき
        sparseMatrix[0].append(i + 1) # sparseMatrixの1つ目の配列にi+1の値を追加する
        sparseMatrix[1].append(j + 1) # sparseMatrixの2つ目の配列にj+1の値を追加する
        sparseMatrix[2].append(matrix[i][j]) # sparseMatrixの3つ目の配列にmatrix[i][j]の値を追加する

2次元配列ではよく2重ループ（ループ処理が重なること）を使います．
2重ループを使うと処理が複雑になる傾向にあるので使っている場合は注意が必要です．

確実に処理を理解するにはトレースをすると良いでしょう．

例えば i=0, j=0, len(matrix)=5の場合を確認します．

for 0 in range(0, 5): # iに0を代入する
  for 0 in range(0, len(matrix[0])): #j=0, matrix[0]=[3, 0, 0, 0, 0]のためlen(matrix[0])は5
    if (matrix[0][0] != 0): # matrix[0][0]=3のため条件式はtrue
        sparseMatrix[0].append(0 + 1) # []（sparseMatrixの1つ目の配列）に1を追加する
        sparseMatrix[1].append(0 + 1) # []（sparseMatrixの2つ目の配列）に1を追加する
        sparseMatrix[2].append(matrix[0][0]) # []（sparseMatrixの3つ目の配列）に3を追加する

続いてi=0, j=1, len(matrix)=5の場合を確認します．
変数jのループは内側にあるため先に処理されることに注意しましょう！

for 0 in range(1, 5): # iに0を代入する
  for 1 in range(0, len(matrix[0])): #j=1, matrix[0]=[3, 0, 0, 0, 0]のためlen(matrix[0])は5
    if (matrix[0][1] != 0): # matrix[0][1]=0のため条件式はfalse 以下の処理は実行されない
        sparseMatrix[0].append(0 + 1) 
        sparseMatrix[1].append(1 + 1)
        sparseMatrix[2].append(matrix[0][1])

複雑な2重ループでも変数を代入していけば処理が理解できそうですね．

2重ループの場合は行単位でループ処理が実行されると覚えておくと便利です．